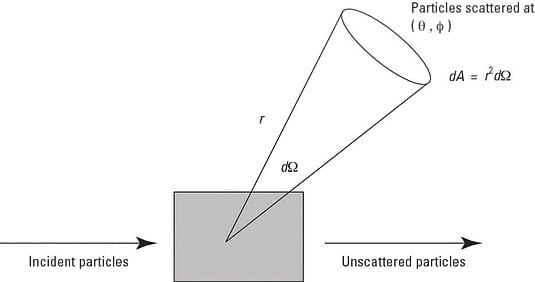
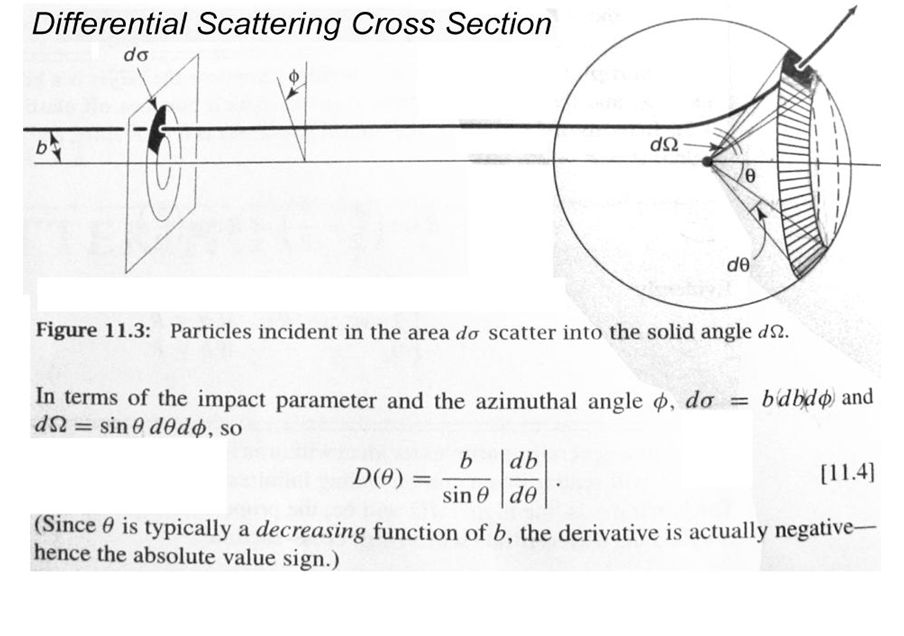
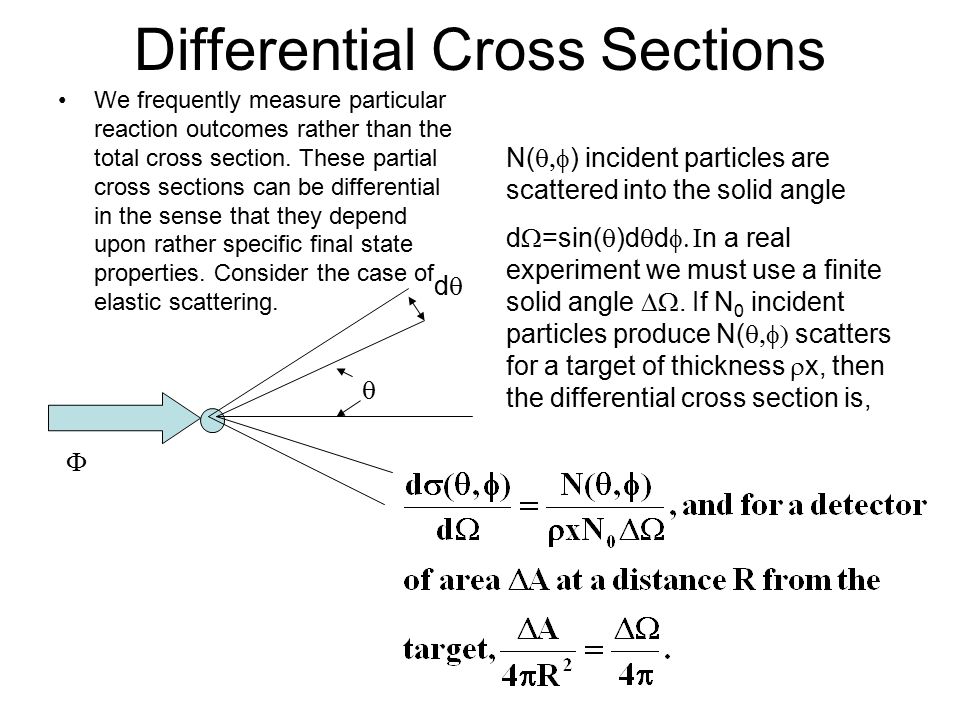
Differential Scattering Cross Section

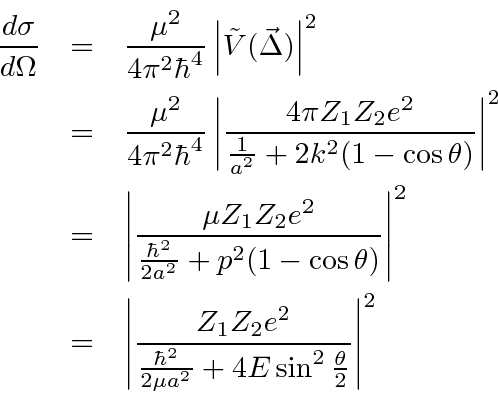
Is expected to be x10.

Differential scattering cross section. The differential scattering cross section scattering intensity of a single electron can be written as 4 3 d σ d ω e b e 2 r e 2 1 cos 2 θ 2 where b e denotes the θ dependent scattering length of a single electron and r e is the radius of the electron 2 818 10 15 m. Here d ω is the spherical surface element. D ω sin θ d θ d ϕ with θ and ϕ the usual angles defined on the sphere which parametrize the outgoing direction of the scattering object.

The differential cross section is extremely useful quantity in many fields of physics as measuring it can reveal a great amount of information about the internal structure of the target particles. The total cross section is the cross section for scattering of any kind through any angle. The scattering cross section is fm2 barns.

So if the differential cross section for scattering to a particular solid angle is like the bull s eye the total cross section corresponds to the whole target. The differential cross section is the cross section for scattering to a specific solid angle. The symbol σ is frequently used for scattering cross section and d σ d ω for the differential cross section.

For example the differential cross section of rutherford scattering provided strong evidence for the existence of the atomic nucleus. With density gm cm3 the scattered fraction for angles greater than degrees. This problem is particularly acute when rayleigh scattering from high pressures of nitrogen is used to calibrate the collection system.

Differential cross section is a measure of the probability that a photon will be scattered within a given small angle. So d sigma which is called the differential cross section differential cross section is equal number of particles there s lots of words here but it s good to write them scattered per unit time into the solid angle d omega divided by the flux of incident particles which is equal to the number of particles per unit area per unit time. For the case of light alpha particles scattering off heavy.

The differential cross section can be derived from the equations of motion for a particle interacting with a central potential in general the equations of motion describing two particles interacting under a central force can be decoupled into the center of mass and the motion of the particles relative to one another. The differential scattering cross section is defined as the ratio of the intensity of radiant energy scattered in a given direction to the incident irradiance and thus has dimensions of area per unit solid angle. The differential cross section for the compton process was derived by the swedish physicist oskar klein and the japanese physicist yoshio nishina.